Omar Gonzàlez Fascinetto (corriente alterna)

yo utilizare el analisis de la corriente alterna como ejemplo de aplicacion de los numeros complejos, lo simplifique lo mas que pude.

corriente alterna:

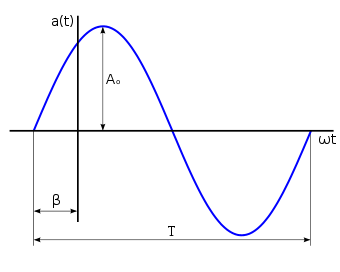
es aquel tipo de corriente cuya magnitud y direccion varian cicliicamente por lo que se puede representar el el plano como una funcion cuya grafica forma una onda sinusoidal:

A0=La amplitud en voltios o amperios
w=la pulsacion en radianes/segundo(esto puede entenderse como una velocidad)
t=tiempo en segundos
β=el angulo de fase en radianes

esta es la grafica resultante



esta funcion tambien puede ser representada por un vector giratorio, a esta representacion se le conoce como representacion fasorial donde el fasor esta dado por un numero complejo de modo que en la evaluacion de sistemas con corriente alterna se pueden usar las peropiedades para el calculo y manejo de estos numeros.



ejemplo:

cuando:

Ao=4 volts
w=1000 radianes/segundo
β=π/4

tenemos que:

por lo tanto:

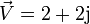
j es un complejo